We have been busy working on determining whether one number is a factor or multiple of another number. We started by building arrays both with tiles and on centimeter grid paper to determine a number's factors. Becoming proficient at building arrays has really helped some of my struggling students feel successful in finding factors even when they aren't proficient in their facts or have many strong strategies to use to determine a fact. After practicing many many times, I gave each student a pair of die (some were six sided, some were more for my kids who are proficient in their facts and wanted a challenge!) and grid paper and instructed them to roll the die and create an array with dimensions that match the numbers on the die. We then added this page to our notebooks. Below is an example.
Next, we used our Math Handbooks and its Table of Contents (oh hello, Language Arts skills! See....I'm learning how to incorporate it all!) to find the definition and examples of factor, prime number, composite number, and square number. We used this information to create a foldable to glue into the right hand side of the page. An example is below!
We are also learning about multiples. After many days of discovering, discussing, and applying this knew knowledge, we finally were able to put the information into our notebooks. I always try to wait until I feel they understand it to put it into the notebooks. We used a hundreds chart to choose a factor, then highlighted all of its multiples. We also used this factor to create a basic real world problem to show how to apply it to multiples.
 |
| This student chose the factor two, and wrote the problem: A store has CDs for $2 each. She then drew a picture to show that one CD would cost $2, two CDs would cost $4, three would cost $6, and so on. This shows that the price of buying CDs are multiples of 2 |
 |
| This student chose the factor four. His problem is about video games costing $4 each, so two would cost $8, three would be $12, and so on. He goes on to begin to write a question associated with it! |
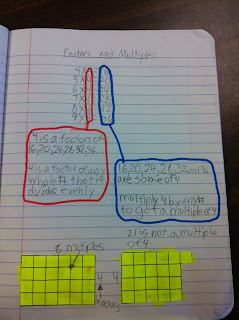
Lastly, I really wanted to make sure we understood the difference between factors and multiples, as it can get very confusing. We used markers to circle all the factors in a list and all the multiples associated with it. Students were allowed to pick their own factor, or for those who are still not feeling comfortable with multiplication, were permitted to use the factor four as I did in my example. Then, they showed an example of an array that shows one of their listed factors and multiples, as well as a non array (just to make sure they understood that an array is a rectangle and cannot have any pieces sticking off the end!!). These last two pages might be my favorite!
 |
| This student wrote all the problems for the number four. He circled all of the fours to show that is the factor. He wrote: 4 is a factor of any whole number that it divides evenly. He also circled all the multiples to show that you can multiply any number by four to get a multiple of four. |
 |
| This student did an excellent job of showing the difference between an array that four is a factor of one of its multiples, as well as a non example saying "21 is not a multiple of 4" and using his array as proof! |
